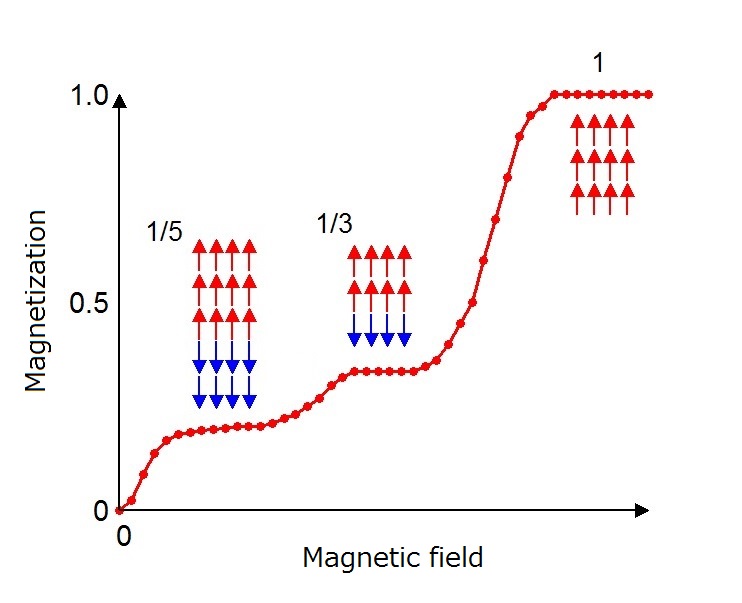
Devil S Staircase Math
Devil S Staircase Math - The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. The graph of the devil’s staircase. The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone. • if [x] 3 contains any 1s, with the first 1 being at position n: Call the nth staircase function. Consider the closed interval [0,1]. Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. [x] 3 = 0.x 1x 2.x n−11x n+1., replace the. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third;
Consider the closed interval [0,1]. • if [x] 3 contains any 1s, with the first 1 being at position n: Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; [x] 3 = 0.x 1x 2.x n−11x n+1., replace the. The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone. The graph of the devil’s staircase. Call the nth staircase function.
The graph of the devil’s staircase. • if [x] 3 contains any 1s, with the first 1 being at position n: Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. Call the nth staircase function. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. Consider the closed interval [0,1]. The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; [x] 3 = 0.x 1x 2.x n−11x n+1., replace the.
Staircase Math
[x] 3 = 0.x 1x 2.x n−11x n+1., replace the. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. • if [x] 3 contains any 1s, with the first 1 being at position n: The devil’s.
Devil's Staircase Continuous Function Derivative
[x] 3 = 0.x 1x 2.x n−11x n+1., replace the. Consider the closed interval [0,1]. The graph of the devil’s staircase. Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third;
The Devil's Staircase science and math behind the music
Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. • if [x] 3 contains any 1s, with the first 1 being at position n: Consider the closed interval [0,1]. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. The first stage of the construction is.
Devil's Staircase by PeterI on DeviantArt
• if [x] 3 contains any 1s, with the first 1 being at position n: [x] 3 = 0.x 1x 2.x n−11x n+1., replace the. The graph of the devil’s staircase. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; The cantor ternary function (also called devil's staircase and,.
Emergence of "Devil's staircase" Innovations Report
The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. The graph of the devil’s staircase. The.
Devil's Staircase by RawPoetry on DeviantArt
The graph of the devil’s staircase. Call the nth staircase function. [x] 3 = 0.x 1x 2.x n−11x n+1., replace the. The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone. Consider the closed interval [0,1].
Devil’s Staircase Math Fun Facts
Call the nth staircase function. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. [x] 3 = 0.x 1x 2.x n−11x n+1., replace the. Consider the closed interval [0,1]. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third;
Devil's Staircase by NewRandombell on DeviantArt
[x] 3 = 0.x 1x 2.x n−11x n+1., replace the. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. Consider the closed interval [0,1]. Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The devil’s staircase is related to the cantor set because by construction.
Devil's Staircase by dashedandshattered on DeviantArt
The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone. • if [x] 3 contains any 1s, with the first 1 being at position n: The graph of the devil’s staircase. Call the nth staircase function. The devil’s staircase is related to the cantor set because by construction d is constant on all.
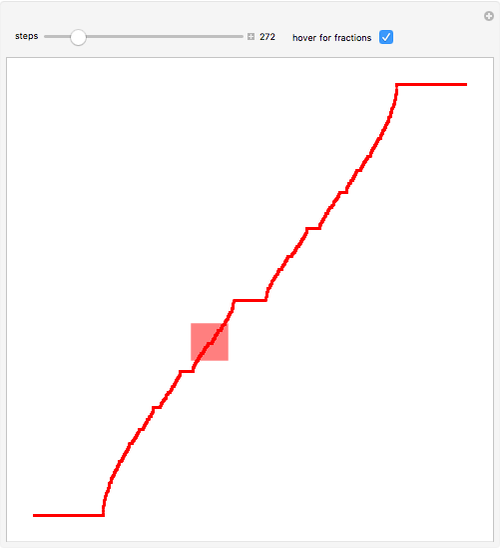
Devil's Staircase Wolfram Demonstrations Project
[x] 3 = 0.x 1x 2.x n−11x n+1., replace the. Call the nth staircase function. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone. The graph of the devil’s staircase.
Consider The Closed Interval [0,1].
[x] 3 = 0.x 1x 2.x n−11x n+1., replace the. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. • if [x] 3 contains any 1s, with the first 1 being at position n: The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone.
The Graph Of The Devil’s Staircase.
Call the nth staircase function. The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}.